Compton Wavelength

Facebook

Author: Thomas Lee Abshier

by Thomas Lee Abshier, ND
10/20/2025

The Compton wavelength is a fundamental physical constant associated with a particle, defined as the wavelength of a photon whose energy is equivalent to the rest energy of the particle. It represents a characteristic quantum mechanical length scale below which quantum effects become significant for describing the particle’s behavior.

Mathematical Definition

The Compton wavelength $\lambda_C$ of a particle is given by the formula:

$\lambda_C = \frac{h}{m c}$

Where:

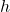$h$ : Planck’s constant ( 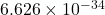$6.626 \times 10^{-34}$ J·s)
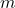$m$ : Rest mass of the particle
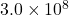$c$ : Speed of light in a vacuum ( $3.0 \times 10^8$ m/s)

Interpretation

Physical Meaning:

The Compton wavelength represents the smallest wavelength of light (photon) that can be used to probe the particle in question without significantly altering its quantum state.
For distances smaller than 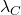$\lambda_C$ , the particle’s quantum nature becomes dominant, and particle-wave duality must be considered.

Relation to Photon-Particle Interaction:

When a photon interacts with a particle (e.g., an electron) via Compton scattering, the wavelength of the scattered photon increases as it transfers energy and momentum to the particle.
The Compton wavelength sets the scale of this wavelength shift and provides a limit to the resolution of a particle’s position using electromagnetic radiation.

Compton Wavelength of an Electron

For an electron, with $m_e = 9.11 \times 10^{-31}$ kg, the Compton wavelength is:

$\lambda_C = \frac{h}{m_e c} = \frac{6.626 \times 10^{-34}}{(9.11 \times 10^{-31})(3.0 \times 10^8)} \approx 2.43 \times 10^{-12} \, \mathrm{m}.$

This is approximately 2.43 picometers, which is very small compared to everyday scales but significant in quantum physics.

Compton Wavelength vs. De Broglie Wavelength

The Compton wavelength is an intrinsic property of a particle and depends only on its rest mass.

The de Broglie wavelength, on the other hand, depends on the particle’s momentum ( $p$ ) and is given by:

$\lambda_{\mathrm{de \, Broglie}} = \frac{h}{p}.$

For a particle at rest, the de Broglie wavelength becomes undefined, while the Compton wavelength remains well-defined.

Significance in Quantum Mechanics

Quantum Field Theory:

The Compton wavelength marks the scale below which quantum field theory becomes essential for describing a particle.
If one tries to localize a particle to a region smaller than 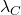$\lambda_C$ , the uncertainty in momentum becomes so large (via Heisenberg’s uncertainty principle) that pair production (creating particle-antiparticle pairs) can occur.

Relativity and Quantum Mechanics:

The Compton wavelength provides a limit to the classical notion of a particle’s size. For example, attempts to probe a particle at scales smaller than 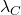$\lambda_C$ would require photons with energy so high that they could create new particles.

Planck Scale:

The Compton wavelength is different from the Planck length, which is the fundamental scale of quantum gravity. However, both represent physical limits to how we understand space and particles at very small scales.

Applications

Compton Scattering:

The Compton wavelength plays a key role in describing the scattering of high-energy photons (like X-rays or gamma rays) off particles such as electrons.

Particle Physics:

It helps set the scale for quantum phenomena and the range of interactions, such as the size of an atom or the resolution limit of a microscope.

Astrophysics:

The Compton wavelength is relevant in processes involving high-energy photons and relativistic particles, such as in black hole accretion disks or cosmic ray interactions.

Summary

The Compton wavelength is a quantum mechanical property of a particle, defined as $\lambda_C = \frac{h}{m c}$ , which depends on the particle’s mass. It represents the smallest length scale at which classical concepts break down and quantum effects dominate. For an electron, the Compton wavelength is approximately 2.43 pm, and it plays a key role in understanding the interaction between particles and electromagnetic radiation, especially in phenomena like Compton scattering.

Compton Wavelength

Author: Thomas Lee Abshier