General Relativity Description and Properties

by | Oct 31, 2025 | Physics, Relativity | 0 comments

Thomas Lee Abshier
Author: Thomas Lee Abshier

Examination of the description of General Relativity

Original Sentence:

Gravity is geometric, with assumptions of diffeomorphism invariance, locality, and the equivalence principle (inertial/gravitational mass equality).

  • This sentence summarizes the philosophical and mathematical foundation of Einstein’s general theory of relativity.

Let’s unpack it piece by piece.

“Gravity is geometric”

  • In general relativity (GR), gravity is not a force in the traditional sense — it is the geometry of spacetime itself.
  • Mass and energy tell spacetime how to curve, and that curvature tells matter and light how to move.

In other words:

  • Gravity ≠ pulling force
  • Gravity = effect of spacetime curvature

When you feel “weight,” you’re following a curved path in spacetime — the geometry itself makes objects move toward one another.

“Diffeomorphism invariance”

  • This is a technical way to say that the laws of physics don’t depend on your coordinate system.
  • A diffeomorphism is a smooth change of coordinates — stretching, relabeling, or deforming spacetime points without tearing or overlapping them.

So, diffeomorphism invariance means:

  • The equations describing gravity remain true no matter how you label points in spacetime.

This is a fundamental symmetry in general relativity — it guarantees that physical laws are the same for all observers, no matter their viewpoint or the coordinates they use.

“Locality”

  • Locality means that physical effects at one point in spacetime are influenced only by what happens nearby, not by distant events instantaneously.

In other words:

  • Interactions propagate continuously through space and time, not instantly across it.
  • This is consistent with special relativity, where nothing (not even information) can travel faster than the speed of light.

In general relativity, locality ensures that the gravitational field at a point depends only on the local curvature of spacetime — determined by the nearby presence of energy and momentum.

“Equivalence principle (inertial/gravitational mass equality)”

  • This is the physical foundation of general relativity.
  • Inertial mass measures how much an object resists acceleration when you push it (Newton’s second law: F = m a).
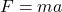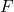    • F: Force
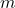    • m: Mass
    • a: Acceleration
  • Gravitational mass measures how strongly an object responds to gravitational attraction.
  • The equivalence principle says that these two quantities are exactly the same:
    • m_{inertial} = m_{gravitational}.
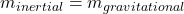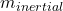    • m_{inertial}: Inertial mass
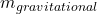    • m_{gravitational}: Gravitational mass
  • That’s why all objects fall at the same rate in a gravitational field, regardless of their mass or composition (ignoring air resistance).

Einstein elevated this observation to a principle:

  • Being in a gravitational field is locally indistinguishable from being in an accelerated frame of reference.
  • That insight led him to reinterpret gravity as spacetime curvature.

Putting It All Together

Gravity is not a force acting through space but a manifestation of the geometry of spacetime itself.

The theory assumes that physical laws are independent of coordinate labels (diffeomorphism invariance), that interactions act locally (locality), and that the equality of inertial and gravitational mass (equivalence principle) holds — leading to the geometric description of gravity as implemented in general relativity.

Simple Summary

  • “Gravity is geometric” → Space and time curve in response to energy and matter.
  • “Diffeomorphism invariance” → The laws don’t depend on coordinates or perspective.
  • “Locality” → Causes influence effects only nearby, not instantaneously at a distance.
  • “Equivalence principle” → Free fall and acceleration are locally indistinguishable; all masses fall equally.

Altogether, these make up the conceptual backbone of Einstein’s general relativity — our best classical theory of gravity.

 

Original Sentence

“GR does not quantize spacetime and breaks down at singularities (e.g., black holes and the Big Bang), requiring an ultraviolet completion.”

This sentence captures one of the most important limitations of general relativity (GR) and why physicists seek a quantum theory of gravity. Let’s unpack it clearly, phrase by phrase.

 

  1. “GR does not quantize spacetime”

    GR (General Relativity) treats spacetime as a smooth, continuous geometric fabric, not as something made of fundamental, discrete elements.

    • GR: General Relativity

    In quantum mechanics (QM), everything — including fields like electromagnetism — has discrete, quantized excitations (photons, for example).

    • QM: Quantum Mechanics

    So:

    GR = classical theory of gravity

    QM = quantum theory of matter and fields

    Unlike quantum theories, GR does not describe spacetime itself as quantized.

    That means it doesn’t account for quantum fluctuations of the gravitational field or how spacetime behaves at extremely small (Planck-scale) distances where quantum effects should dominate.

  2. “and breaks down at singularities (e.g., black holes and the Big Bang)”

    A singularity is a point (or region) in spacetime where the equations of GR predict that physical quantities like density, curvature, or energy become infinite — which means the theory stops making sense there.

    Examples:

    Inside a black hole at the center (the “singularity” inside the event horizon).

    At the Big Bang, where the density of the early universe would be infinite.

    At singularities, GR no longer provides finite, physically meaningful predictions.

    That’s why we say it “breaks down” — the mathematics of GR ceases to describe reality.

  3. “requiring an ultraviolet completion”

    Let’s break that into two parts:

    (a) Ultraviolet (UV):

    In physics, “ultraviolet” is shorthand for very high energy or very short distance scales.

    • UV: Ultraviolet

    “Infrared” (IR) refers to low energy or long distance scales.

    • IR: Infrared

    As you probe shorter and sho-rter distances (higher energies), quantum effects usually become more important.

    (b) Completion:

    A completion of a theory means an extension or replacement that remains valid where the original theory fails.

    Thus, an ultraviolet completion of general relativity is:

    A more fundamental theory that stays valid at very high energies / very short distances — where GR breaks down.

    In this context, “ultraviolet completion” refers to a future quantum theory of gravity — one that describes how spacetime behaves quantum-mechanically, resolving the singularities and inconsistencies of classical GR.

    Possible candidates for this completion include:

    • String theory
    • Loop quantum gravity
    • Causal sets, asymptotic safety, and other quantum-gravity models

Putting It All Together

General relativity describes gravity as classical spacetime curvature, not as a quantized field. However, this classical description fails at singularities—like those inside black holes or at the Big Bang—where spacetime curvature becomes infinite. To correctly describe gravity at these extreme, high-energy (ultraviolet) scales, we need a more fundamental quantum theory, known as an ultraviolet completion.

Simplified Summary

  • GR is classical, not quantum — spacetime isn’t quantized in it.
  • GR breaks down at singularities, where it predicts infinities (inside black holes, at the Big Bang).
  • Therefore, a deeper theory (a “UV completion”) is needed to describe gravity at extremely high energies and small scales — a quantum theory of gravity.

In One Sentence

General relativity treats spacetime classically, but this description fails where spacetime curvature becomes infinite, so a more fundamental, quantum theory valid at very high energies (an ultraviolet completion) is required.

 

 

Submit a Comment