Transition from Linear to Chaotic Systems

Transition from Linear to Chaotic Systems
by Thomas Lee Abshier, ND, and Poe Assistant
7/30/2025

The transition from laminar flow to turbulence in fluid dynamics, and more broadly from linear to chaotic systems, represents a shift from predictable, ordered behavior to complex, unpredictable dynamics. This transition is key to understanding a wide range of phenomena, from airflow over airplane wings to weather patterns, and is governed by nonlinear interactions.

---

1. Laminar Flow vs. Turbulent Flow

Laminar Flow

• Definition: A smooth, orderly flow regime where fluid moves in parallel layers with little to no mixing between them.
• Characteristics:
  • Velocity at a given point is constant over time.
  • Streamlines (paths traced by fluid particles) are parallel and do not intersect.
  • Described by linear equations (e.g., Navier-Stokes equations for low Reynolds numbers).
• Example: Flow of honey or water moving slowly through a pipe.

Turbulent Flow

• Definition: A chaotic, disordered flow regime characterized by rapid mixing, vortices, and eddies.
• Characteristics:
  • Velocity at a given point fluctuates in magnitude and direction.
  • Streamlines break down, intersect, and create complex patterns.
  • Governed by nonlinear dynamics and sensitive to initial conditions.
• Example: Smoke rising from a flame, atmospheric wind patterns, or fast-moving water in rivers.

---

2. Transition from Laminar to Turbulent Flow

The transition from laminar to turbulent flow is influenced by the Reynolds number ($Re$), a dimensionless quantity that characterizes the relative importance of inertial forces to viscous forces in a fluid:

where:

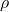• $\rho$: Fluid density,
• $v$: Flow velocity,
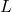• $L$: Characteristic length scale (e.g., pipe diameter),
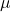• $\mu$: Dynamic viscosity of the fluid.

Key Stages of the Transition:

1. Low Reynolds Number ($Re < 2000$):
   • Flow is laminar, dominated by viscous forces. Disturbances are damped out.
2. Critical Reynolds Number ($Re \sim 2000-4000$):
   • Flow becomes unstable, and small perturbations (e.g., vibrations, surface roughness) are amplified.
   • Transitional flow emerges, with intermittent turbulence.
3. High Reynolds Number ($Re > 4000$):
   • Flow becomes fully turbulent, dominated by inertial forces.
   • Energy cascades from large eddies (where energy is injected) to smaller scales, eventually dissipating as heat due to viscosity.

Physical Mechanisms Behind the Transition:

• Instabilities: Small perturbations in the flow (e.g., boundary layer instabilities) grow due to nonlinear interactions.
• Nonlinear Coupling: Nonlinear terms in the Navier-Stokes equations cause interactions between velocity components, leading to chaotic behavior.
• Energy Cascade: Energy flows from large-scale coherent structures (like vortices) to smaller, chaotic eddies.

---

3. Transition from Linear to Chaotic Systems

The transition from linear to chaotic behavior is a general feature of many dynamical systems where nonlinearities dominate. While laminar-turbulent flow transition is a specific example, the broader framework of chaos theory applies universally.

Linear Systems

• Definition: Systems where the output is directly proportional to the input, and superposition applies.
• Characteristics:
  • Predictable and solvable using analytical methods.
  • Governed by linear equations (e.g., Hooke’s law, simple harmonic oscillators).
• Example: A pendulum swinging with small amplitudes.

Nonlinear Systems

• Definition: Systems where outputs are not proportional to inputs and small changes can lead to large effects.
• Characteristics:
  • sensitive dependence on initial conditions.
  • Governed by nonlinear equations with feedback mechanisms.
  • May exhibit chaos, where predictability is lost over time.
• Example: A pendulum swinging at large amplitudes, weather systems, or population dynamics.

---

4. The Path to Chaos

The transition to chaos in nonlinear systems can occur through several mechanisms. These mechanisms are often observed in fluid dynamics, electrical circuits, and other physical systems.

a. Bifurcations

• Small changes in system parameters cause qualitative changes in behavior.
• Example: In fluid systems, increasing $Re$ leads to a sequence of bifurcations, such as:
  1. Steady State: Laminar flow.
  2. Periodic Oscillations: Regular vortices (e.g., von Kármán vortex street).
  3. Quasi-periodic Behavior: Multiple incommensurate frequencies.
  4. Chaos: Irregular, aperiodic behavior.

b. Sensitive Dependence on Initial Conditions

• In chaotic systems, small differences in initial conditions grow exponentially over time, leading to unpredictable outcomes.
• Example: Weather systems (the “butterfly effect”).

c. Nonlinear Feedback

• Feedback loops amplify small perturbations, leading to complex dynamics.
• Example: In turbulence, interactions between scales create cascades of energy.

---

5. Laminar-Turbulent Transition as a Chaotic System

The transition from laminar flow to turbulence is an example of a system becoming chaotic. Here’s how it aligns with chaos theory:

1. Nonlinearity:
   • The Navier-Stokes equations for fluid motion are inherently nonlinear.
   • Nonlinear terms couple velocity components, amplifying small disturbances.
2. Bifurcations in Flow:
   • As 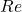$Re$ increases, flow evolves from steady laminar behavior to periodic oscillations, quasi-periodicity, and eventually chaotic turbulence.
3. Phase Space and Attractors:
   • Laminar flow corresponds to a stable fixed point in phase space.
   • Turbulence corresponds to a strange attractor, a fractal structure that describes the chaotic behavior of the system.
4. Energy Cascade:
   • In turbulence, large vortices break down into smaller eddies in a process governed by nonlinear interactions.

---

6. Broader Implications of the Transition

The transition from laminar to turbulent flow, and from linear to chaotic systems, is a universal phenomenon with applications beyond fluid dynamics:

1. Engineering:
   • Designing efficient systems (like airplane wings or pipelines) requires understanding turbulence to minimize drag.
2. Climate and Weather:
   • Atmospheric turbulence and chaotic behaviors influence weather prediction.
3. Biological Systems:
   • Blood flow in arteries can transition to turbulence under certain conditions.
   • Population dynamics can exhibit chaotic behavior in predator-prey systems.
4. Physics and Cosmology:
   • Understanding turbulence is crucial for plasma physics, astrophysical phenomena (e.g., accretion disks), and galaxy formation.

---

7. Summary

• The transition from laminar flow to turbulence is a specific example of a broader transition from linear to chaotic systems.
• Laminar flow is smooth and predictable, while turbulent flow is chaotic, with vortices and energy cascades.
• The transition is driven by nonlinearities in the governing equations, such as the Navier-Stokes equations, and is heavily influenced by the Reynolds number.
• This transition reflects fundamental principles of chaos theory, including bifurcations, sensitive dependence on initial conditions, and strange attractors.

Understanding these transitions is crucial for applications across physics, engineering, biology, and beyond.