The Electron g-2 Explained

by | Nov 3, 2025 | Physics, Quantum Mechanics | 0 comments

Thomas Lee Abshier
Author: Thomas Lee Abshier

The Electron g-2 in QED

QED is a cornerstone topic in modern physics. The following is an explanation of what QED corrections are and what the famous electron g-2 means, step by step.

1. Background: What is QED?

Quantum Electrodynamics (QED) is the quantum field theory of the electromagnetic force.

It describes how charged particles — such as electrons and positrons — interact with light (photons) via the exchange of virtual photons.

QED combines:

  • Quantum mechanics (wave-particle duality, probabilities), and
  • Special relativity (Einstein’s theory of space and time), with
  • Electromagnetism (Maxwell’s equations).

It’s one of the most accurate and experimentally verified theories in physics.

2. What Are QED Corrections?

  • In classical electrodynamics, an electron is just a point charge interacting with the electromagnetic field.
  • But in quantum electrodynamics, the vacuum isn’t empty — it’s teeming with virtual particles that appear and disappear instantaneously.
  • An electron, therefore, isn’t “bare”: it’s surrounded by a cloud of virtual photons, electron–positron pairs, and other quantum effects.
  • These modify (or “renormalize”) its observable properties — such as its charge, mass, and magnetic moment.
  • These small modifications are the QED corrections.

3. Magnetic Moment and the 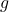g-Factor

An electron behaves like a tiny spinning magnet, producing a magnetic dipole moment:

\mu = g \left( \frac{e \hbar}{2 m_e} \right) S

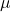  • \mu: magnetic moment
  • e: charge of the electron
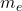  • m_e: electron mass
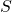  • S: spin angular momentum
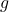  • g: gyromagnetic ratio (dimensionless factor)

The Dirac Prediction In Dirac’s original relativistic quantum theory of the electron (1928):

g = 2

  • So Dirac’s theory predicts that the electron’s magnetic moment should be exactly twice the classical value expected for a spinning charged particle.
  • The QED Correction: g-2 Experiments found the actual magnetic moment is slightly larger than 2.
  • The difference is called the anomalous magnetic moment:
  • a_e = \frac{g-2}{2}
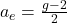
  • This tiny deviation from 2 arises entirely from QED corrections — the effects of virtual particles influencing how the electron interacts with the electromagnetic field.

4. Where the Correction Comes From

  • In QED, electron interactions are represented as Feynman diagrams.
  • At higher orders, you include additional “loop” diagrams.
  • The first correction comes from the one-loop vertex diagram:
  • simplified Feynman diagram showing vertex correction — an electron emits and reabsorbs a virtual photon
  • It describes the electron briefly emitting and reabsorbing a virtual photon.
  • These higher-order “loops” slightly shift the predicted magnetic moment.
  • The lowest-order correction was calculated by Julian Schwinger (1948):
  • a_e = \frac{\alpha}{2 \pi} \approx 0.0011614
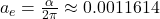
  • where 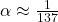\alpha \approx \frac{1}{137} is the fine-structure constant.

5. Modern Precision

  • QED has since been developed to include corrections up to fifth-order loops and beyond.
  • The theoretical prediction for 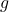g agrees with experiments to better than one part in 10 trillion — the most precise agreement between theory and experiment in all of science.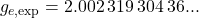
  • g_{e, \exp} = 2.002 \, 319 \, 304 \, 36...
  • and theory gives the same result to astounding precision:
  • g_{e, \theory} = 2.002 \, 319 \, 304 \, 35...
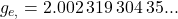
  • This level of precision indirectly measures the fine-structure constant 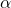\alpha and provides stringent tests for physics beyond the Standard Model.

6. Why This Matters

  • QED corrections explain why the electron’s magnetic moment isn’t exactly 2.
  • They illustrate how quantum fluctuations of the vacuum modify measurable properties.
  • The match between QED theory and experiment is one of the biggest triumphs of modern physics.
  • Any deviation in future measurements (like in the muon g-2 anomaly) could signal new physics, such as supersymmetry or undiscovered particles.

Summary

Term Meaning
QED corrections Adjustments to particle properties due to quantum fluctuations and loop diagrams.
Dirac prediction g = 2 for a pointlike spin-½ particle.
Schwinger correction a_e = \frac{\alpha}{2 \pi} — first QED correction to g.
Anomalous magnetic moment a_e = \frac{g-2}{2} — difference from the Dirac value.
Significance QED predictions match experiments to ≈ 1 part in 10¹³; tests the limits of the Standard Model.

QED corrections account for the tiny quantum “fuzz” around the electron that slightly alters its magnetic moment, giving g-2 \neq 0; this small shift, predicted and measured with extreme precision, is one of the greatest validations of quantum field theory.

 

Submit a Comment