The Fermi Gas and Stellar Collapse
By Thomas Lee Abshier, ND, and Poe Assistant
7/21/2025
Assistant
The Fermi gas is a physical model used in quantum mechanics and statistical physics to describe a system of many non-interacting fermions (particles that obey the Pauli exclusion principle). It is primarily applied to systems such as electrons in metals, neutrons in neutron stars, or atoms in ultracold Fermi gases. Here’s a detailed breakdown of the concept:
1. What is a Fermi Gas?
A Fermi gas consists of a collection of fermions (particles with half-integer spin, such as electrons, neutrons, or protons) at absolute zero temperature or finite temperatures.
The key features of fermions:
- Pauli Exclusion Principle: No two identical fermions can occupy the same quantum state simultaneously.
- Quantum Statistics: Fermions are described by Fermi-Dirac statistics, which determine how these particles distribute themselves among the available quantum states.
In the simplest Fermi gas model:
- The particles are non-interacting (their potential energy does not significantly affect the system).
- The particles are confined to a specific volume and obey quantum mechanical rules.
2. Quantum States in a Fermi Gas
a. Energy Levels
- In a quantum system, particles occupy discrete energy levels.
- For a gas of fermions, the available quantum states are filled in order of increasing energy, starting from the lowest state.
b. Fermi Energy (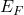 )
)
- The Fermi energy is the highest energy level occupied by a fermion at absolute zero temperature.
- At zero temperature:
- All quantum states with energy less than
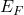 are fully occupied.
are fully occupied. - All states with energy greater than
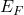 are empty.
are empty.
- All quantum states with energy less than
c. Fermi Surface
- In momentum space, the Fermi surface is the boundary separating the occupied and unoccupied states at
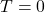 .
. - The states inside the Fermi surface are occupied, while those outside are empty.
3. Properties of a Fermi Gas
a. Degeneracy Pressure
- Even at absolute zero, a Fermi gas exerts a pressure known as degeneracy pressure due to the Pauli exclusion principle.
- This pressure arises because fermions cannot all occupy the lowest energy state—they must “stack” into higher energy states.
- Degeneracy pressure plays a critical role in systems such as:
- White dwarfs (electron degeneracy pressure prevents collapse).
- Neutron stars (neutron degeneracy pressure prevents collapse).
b. Density of States
- The density of states describes the number of quantum states available per unit energy and volume.
- For a three-dimensional Fermi gas:
![]()
meaning the number of states increases with energy.
4. Fermi-Dirac Distribution
At finite temperatures, the occupation of energy states is described by the Fermi-Dirac distribution:
![]()
where:
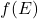 : Probability of a state with energy
: Probability of a state with energy 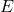 being occupied.
being occupied.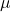 : Chemical potential (approximately the Fermi energy at low temperatures).
: Chemical potential (approximately the Fermi energy at low temperatures).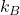 : Boltzmann constant.
: Boltzmann constant.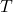 : Temperature.
: Temperature.
Key features:
- At
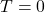 ,
, 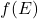 is a step function:
is a step function: 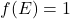 for
for 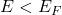 , and
, and 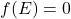 for
for 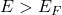 .
. - At
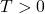 , the step function smoothens as thermal energy allows some particles to occupy higher energy states.
, the step function smoothens as thermal energy allows some particles to occupy higher energy states.
5. Applications of the Fermi Gas Model
a. Electrons in Metals
In a metal, conduction electrons behave like a Fermi gas:
- The electrons occupy quantum states up to the Fermi energy.
- The model explains properties such as electrical conductivity, heat capacity, and thermal conductivity.
b. Neutron Stars
In neutron stars, neutrons are densely packed and behave like a Fermi gas.
- Neutron degeneracy pressure, arising from the Pauli exclusion principle, prevents the star from collapsing under gravity (unless the mass exceeds the Tolman-Oppenheimer-Volkoff limit).
c. Ultracold Fermi Gases
Atoms cooled to near absolute zero can form a quantum degenerate Fermi gas.
- These systems are studied to explore quantum phenomena like superfluidity and pairing mechanisms (related to superconductivity).
6. Mathematical Description
a. Fermi Energy
The Fermi energy for a three-dimensional Fermi gas is given by:
![]()
where:
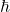 : Reduced Planck’s constant.
: Reduced Planck’s constant.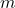 : Mass of the fermion.
: Mass of the fermion.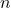 : Number density of fermions.
: Number density of fermions.
b. Total Energy at 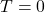
The total energy of the Fermi gas at absolute zero is:
![]()
where ![]() is the total number of fermions.
is the total number of fermions.
c. Heat Capacity
At low temperatures, the heat capacity of a Fermi gas is proportional to the temperature:
![]()
This differs from a classical gas, where ![]() is constant.
is constant.
7. Limitations of the Fermi Gas Model
- The Fermi gas model assumes non-interacting particles, which is an approximation.
- Interactions between particles (e.g., electron-electron repulsion in metals) require more sophisticated models, such as the Fermi liquid theory.
- For very dense systems, strong nuclear forces or other interactions may dominate, as in neutron stars.
Summary
The Fermi gas is a model that describes a collection of non-interacting fermions obeying quantum mechanical and statistical rules. It is characterized by:
- The Pauli exclusion principle forces fermions to occupy distinct quantum states.
- A Fermi energy that marks the highest occupied energy level at absolute zero.
- A Fermi-Dirac distribution that governs the occupation of energy states at finite temperatures.
This model is fundamental in explaining the behavior of electrons in metals, the stability of neutron stars, and the properties of ultracold quantum gases. It serves as a cornerstone of modern quantum and statistical physics!
2:41 AM 6/21/2025
Assistant
The Fermi gas model plays a crucial role in understanding the structure and stability of white dwarf stars, which are dense remnants of stars that have exhausted their nuclear fuel. Here’s a detailed explanation of how the model applies to white dwarfs:
1. What is a White Dwarf?
- A white dwarf is the end stage of a low- to medium-mass star (up to about 8 solar masses).
- After the star burns its nuclear fuel, its outer layers are ejected, leaving behind a dense core primarily composed of carbon and oxygen.
- The core is extremely compact, with a mass comparable to the Sun but a radius similar to Earth.
- The density of a white dwarf is extraordinarily high:
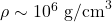 , meaning electrons and nuclei are packed very closely together.
, meaning electrons and nuclei are packed very closely together.
2. Role of the Fermi Gas in a White Dwarf
a. Electron Degeneracy Pressure
In a white dwarf, the electrons form a Fermi gas because:
- Electrons are fermions, so they obey the Pauli exclusion principle.
- The extreme density forces electrons into higher and higher momentum states as lower-energy states are filled.
- Even at absolute zero temperature, the electrons occupy a range of energy levels up to the Fermi energy.
The degeneracy pressure arises from the quantum mechanical behavior of the electron Fermi gas:
- The Pauli exclusion principle prevents electrons from collapsing into the same quantum state, creating a pressure that resists further compression.
- This pressure, called electron degeneracy pressure, is independent of temperature and depends only on the density of the electron gas.
b. Balancing Gravity
- A white dwarf remains stable because the inward pull of gravity is balanced by the outward electron degeneracy pressure.
- Without degeneracy pressure, the star would collapse under its own gravity.
3. The Physics of the Electron Fermi Gas in White Dwarfs
a. Non-Relativistic Fermi Gas
At low densities, where the electrons are moving at speeds much less than the speed of light, the electron degeneracy pressure is described by:
![]()
where ![]() is the mass density.
is the mass density.
This relationship is derived from the Fermi gas model for non-relativistic electrons.
b. Relativistic Fermi Gas
At very high densities, the electrons become relativistic (their speeds approach the speed of light). In this regime:
![]()
Relativistic degeneracy pressure increases more slowly with density than non-relativistic degeneracy pressure, which has profound implications for the stability of the white dwarf (discussed below).
4. Chandrasekhar Limit
- The Chandrasekhar limit is the maximum mass of a white dwarf that can be supported by electron degeneracy pressure.
- As the mass of the white dwarf increases, its density increases, and the electrons become relativistic. In the relativistic regime, the degeneracy pressure
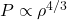 is insufficient to balance gravity for masses above a critical value.
is insufficient to balance gravity for masses above a critical value.
The Chandrasekhar limit is approximately:
![]()
where ![]() is the mass of the Sun.
is the mass of the Sun.
White dwarfs with masses below this limit remain stable. Those exceeding the limit collapse further, potentially forming a neutron star or triggering a Type Ia supernova.
5. Energy and Temperature in a White Dwarf
a. Temperature Independence of Degeneracy Pressure
- Unlike a classical gas, the electron degeneracy pressure in a Fermi gas does not depend on temperature. This is because the pressure arises from the quantum mechanical exclusion principle, not thermal motion.
- As a result, even as the white dwarf cools over time, the degeneracy pressure remains sufficient to support the star.
b. Cooling of White Dwarfs
- White dwarfs radiate energy as they slowly cool over billions of years, eventually becoming faint black dwarfs.
- The cooling is governed by the thermal energy of the nuclei (ions), not the electrons, as the electrons are already in a degenerate state.
6. Relativistic Effects and Instability
- Relativistic degeneracy becomes important as the density of a white dwarf approaches the Chandrasekhar limit.
- In the relativistic regime, the pressure no longer increases fast enough with density to counteract the gravitational force. This leads to:
- Instability: If the mass exceeds
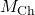 , gravity overwhelms degeneracy pressure, resulting in collapse.
, gravity overwhelms degeneracy pressure, resulting in collapse. - The collapse forms a neutron star (if the mass is sufficient to compress protons and electrons into neutrons) or triggers a Type Ia supernova if the white dwarf accretes matter from a companion star.
- Instability: If the mass exceeds
7. Summary of the Fermi Gas Model’s Role
The Fermi gas model provides the theoretical foundation for understanding electron degeneracy pressure, which supports white dwarfs against gravitational collapse.
The model explains:
- Why white dwarfs are stable below the Chandrasekhar limit.
- The relationship between density and pressure, including the transition from non-relativistic to relativistic regimes.
- The ultimate fate of white dwarfs, including their collapse into neutron stars or supernova explosions if the Chandrasekhar limit is exceeded.
The Fermi gas model is thus essential to the study of stellar remnants and compact objects in astrophysics. Let me know if you’d like a deeper dive into any specific aspect of white dwarfs or Fermi gases! 😊
3:06 AM 7/21/2025
Assistant
The Fermi gas model is crucial for understanding the structure and stability of neutron stars, which are the remnants of massive stars that have undergone supernova explosions. Neutron stars are extremely dense objects, where the behavior of neutrons (and other particles) as a degenerate Fermi gas governs their physical properties, including pressure, density, and size. Here’s how the model applies:
1. What is a Neutron Star?
- A neutron star forms when the core of a massive star (8–25 times the Sun’s mass) collapses under gravity during a supernova.
- The density of a neutron star is immense:
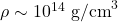 , comparable to the density of an atomic nucleus.
, comparable to the density of an atomic nucleus. - The star is primarily composed of neutrons, with some protons, electrons, and possibly exotic particles like hyperons or quark matter in its core.
2. Role of the Fermi Gas Model
The Fermi gas model provides a theoretical framework to describe the behavior of neutrons, protons, and electrons in the star under conditions of extreme density and pressure.
a. Neutrons as a Fermi Gas
- Neutrons are fermions (spin-
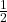 ) and obey the Pauli exclusion principle, meaning no two neutrons can occupy the same quantum state.
) and obey the Pauli exclusion principle, meaning no two neutrons can occupy the same quantum state. - In a neutron star, the neutrons are tightly packed, forming a highly dense degenerate Fermi gas.
- The degeneracy pressure of this neutron gas resists further gravitational collapse and provides stability to the star.
b. Electrons and Protons in the Fermi Gas
- In addition to neutrons, electrons and protons in the star also behave as degenerate Fermi gases, especially in the outer layers (crust).
- The electrons play an important role in maintaining charge neutrality with the protons.
3. Degeneracy Pressure in Neutron Stars
a. What is Degeneracy Pressure?
- Degeneracy pressure is the quantum mechanical pressure exerted by fermions due to the Pauli exclusion principle.
- Even at absolute zero temperature, fermions occupy a range of momentum states up to the Fermi momentum (
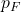 ), creating pressure that resists compression.
), creating pressure that resists compression.
b. Non-Relativistic Degeneracy Pressure
For low densities, where the neutrons are moving at speeds much less than the speed of light, the degeneracy pressure is given by:
![]()
where ![]() is the mass density.
is the mass density.
This behavior is similar to electrons in white dwarfs but with much higher densities and masses.
c. Relativistic Degeneracy Pressure
At extremely high densities, the neutrons become relativistic (their speeds approach the speed of light), and the degeneracy pressure scales differently:
![]()
Relativistic degeneracy pressure increases more slowly with density than non-relativistic pressure, which has important implications for the stability of neutron stars.
4. Equation of State (EoS) for Neutron Stars
The equation of state (EoS) relates pressure (![]() ) to density (
) to density (![]() ) and is a key property of neutron stars:
) and is a key property of neutron stars:
- The Fermi gas model provides a theoretical basis for the EoS, incorporating the effects of neutron degeneracy pressure.
- For a simple degenerate neutron gas:
![]()
where ![]() is the Fermi momentum and
is the Fermi momentum and ![]() is the neutron mass.
is the neutron mass.
- The EoS determines the star’s mass-radius relationship and maximum mass.
5. Stability of Neutron Stars and the Tolman-Oppenheimer-Volkoff (TOV) Limit
a. Balancing Gravity and Degeneracy Pressure
Neutron stars are supported by the balance between:
- Gravitational Pressure: The inward pull due to gravity.
- Degeneracy Pressure: The outward push from the degenerate Fermi gas of neutrons.
If the gravitational force exceeds the degeneracy pressure, the star will collapse.
b. TOV Limit
The Tolman-Oppenheimer-Volkoff limit is the maximum mass of a neutron star that can be supported by neutron degeneracy pressure.
The TOV limit is approximately:
![]()
where ![]() is the mass of the Sun.
is the mass of the Sun.
If a neutron star’s mass exceeds this limit (e.g., due to accretion or merging), it will collapse into a black hole or possibly a quark star.
6. Composition and Structure of Neutron Stars
a. Crust
- The outer layers of a neutron star consist of a lattice of nuclei and a degenerate Fermi gas of electrons.
- As density increases, electrons become ultra-relativistic, and neutrons begin to drip out of nuclei, forming a neutron-rich crust.
b. Core
The core of a neutron star is composed of a degenerate Fermi gas of neutrons, with some protons and electrons.
At higher densities, exotic states of matter may form:
- Hyperons: Particles containing strange quarks.
- Quark Matter: A deconfined Fermi gas of up, down, and strange quarks.
- Color Superconductivity: A paired state of quarks analogous to superconducting electrons.
7. Temperature Effects in Neutron Stars
a. Initial Heat
- Newly formed neutron stars are extremely hot (
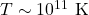 ), but the degeneracy pressure is almost entirely independent of temperature.
), but the degeneracy pressure is almost entirely independent of temperature. - The temperature primarily affects the thermal motion of particles within the star.
b. Cooling
Neutron stars cool rapidly via neutrino emission processes, such as:
- Direct Urca process:
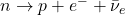 ,
, 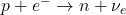 .
. - Modified Urca process: Similar, but involving an additional nucleon to conserve momentum.
After a few million years, the star cools to ![]() , and surface radiation becomes the dominant cooling mechanism.
, and surface radiation becomes the dominant cooling mechanism.
8. Relativistic Effects and General Relativity
- Neutron stars are compact objects where general relativity plays a critical role.
- The Fermi gas model is modified by relativistic effects, including:
- The curvature of spacetime due to gravity.
- The requirement to solve the Tolman-Oppenheimer-Volkoff equation to determine the star’s structure.
9. Summary of the Fermi Gas Model in Neutron Stars
The Fermi gas model is essential for describing the behavior of particles in neutron stars:
Degenerate Neutrons:
- The neutrons form a degenerate Fermi gas, whose pressure counteracts gravitational collapse.
Relativistic Effects:
- At extreme densities, the neutrons become relativistic, affecting the equation of state and the star’s stability.
Mass and Stability:
- The balance between degeneracy pressure and gravity determines the maximum mass of a neutron star (TOV limit).
Extensions:
- The model can be extended to include exotic matter (hyperons, quark matter) in the star’s core.
This model provides a framework for understanding the extreme environments within neutron stars and their evolution into black holes or quark stars. Let me know if you’d like to explore any specific aspect further! 😊
3:17 AM 7/21/2025
Assistant
The Fermi gas model provides a foundation for understanding the behavior of fermions (quarks) in a quark-gluon plasma (QGP), a state of matter thought to exist under extreme conditions of temperature and density, such as in the cores of neutron stars or during the transition between neutron stars and black holes. Here’s how the Fermi gas model applies to these systems:
1. What is a Quark-Gluon Plasma?
A quark-gluon plasma (QGP) is a state of matter where quarks and gluons, the fundamental constituents of protons and neutrons, are no longer confined into hadrons (protons, neutrons, etc.) but exist as a free, deconfined plasma.
A QGP forms at extremely high:
- Densities: Found in the cores of neutron stars or during the collapse of massive stars.
- Temperatures: Created in heavy-ion collisions, such as those conducted at the Large Hadron Collider (LHC) or Relativistic Heavy Ion Collider (RHIC).
The Fermi gas model is used to describe the behavior of quarks in this deconfined plasma.
2. Application of the Fermi Gas Model to a Quark-Gluon Plasma
a. Quarks as Fermions
- Quarks are spin-
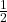 particles and obey the Pauli exclusion principle, meaning they must occupy distinct quantum states.
particles and obey the Pauli exclusion principle, meaning they must occupy distinct quantum states. - In a QGP, quarks form a Fermi gas:
- The quarks occupy energy states up to the Fermi energy.
- Their distribution follows Fermi-Dirac statistics:
![]()
where ![]() is the energy of a state,
is the energy of a state, ![]() is the chemical potential, and
is the chemical potential, and ![]() is the temperature.
is the temperature.
b. High-Density Environment
- In extreme environments like the cores of neutron stars, quark densities are so high that the Fermi energy of the quarks is very large.
- The pressure in such a system is dominated by quark degeneracy pressure, arising from the Pauli exclusion principle for quarks.
c. Deconfinement of Quarks
- Normally, quarks are confined within protons and neutrons due to the strong nuclear force (mediated by gluons).
- At high enough densities (or temperatures), the strong force weakens due to asymptotic freedom, allowing quarks to move freely in a plasma state.
- The deconfined quarks still behave like a Fermi gas, but the interactions between them (mediated by gluons) must also be considered.
3. Key Features of the Fermi Gas Model in QGPs
a. Degeneracy Pressure
- In a QGP, quark degeneracy pressure plays a central role in counteracting gravitational collapse.
- The pressure is given by the distribution of quarks in momentum space, similar to the case for electrons in white dwarfs or neutrons in neutron stars.
b. Energy and Density Relations
For a non-relativistic Fermi gas (low densities), the pressure scales as:
![]()
where ![]() is the density.
is the density.
For a relativistic Fermi gas (high densities, where quarks move at speeds close to the speed of light), the pressure scales as:
![]()
These equations govern the equation of state (EoS) of the QGP, which determines how pressure and density relate in the system.
c. Fermi Momentum and Energy
- The Fermi momentum (
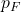 ) and Fermi energy (
) and Fermi energy (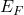 ) of quarks are very high in a QGP due to the extreme densities. These quantities determine the thermodynamic properties of the plasma.
) of quarks are very high in a QGP due to the extreme densities. These quantities determine the thermodynamic properties of the plasma.
d. Temperature Effects
At high temperatures, the Fermi gas model is modified by thermal contributions:
- The quark distribution spreads out beyond the Fermi surface.
- Thermal excitations allow quarks to occupy higher momentum states.
4. Transition Between Neutron Stars and Black Holes
a. Formation of QGP in Neutron Stars
- In neutron stars, as density increases (e.g., due to accretion or collapse), the neutrons themselves may break apart into their constituent quarks, forming a quark core surrounded by a neutron-rich outer layer.
- This “hybrid star” has a QGP core that can be described as a relativistic Fermi gas of quarks.
b. Collapse to a Black Hole
- If the mass of the neutron star exceeds the Tolman-Oppenheimer-Volkoff (TOV) limit, even the degeneracy pressure from quarks cannot counteract gravity, leading to the formation of a black hole.
- The transition from a QGP to a black hole involves extreme compression, where even the Fermi gas description may break down as general relativity dominates.
5. Equation of State for a QGP
The equation of state (EoS) describes the relationship between pressure, density, and temperature. For a QGP:
- At low densities, the EoS resembles that of a non-relativistic Fermi gas.
- At high densities, the EoS transitions to a relativistic Fermi gas:
![]()
where ![]() is the energy density, characteristic of a relativistic plasma.
is the energy density, characteristic of a relativistic plasma.
The EoS is critical for understanding:
- The structure and stability of neutron stars with quark cores.
- The threshold for collapse into a black hole.
6. Interactions in a Fermi Gas of Quarks
Unlike a traditional ideal Fermi gas, a QGP includes interactions between quarks mediated by gluons:
- Strong Interactions: Quarks interact through the strong nuclear force, which is described by Quantum Chromodynamics (QCD).
- Screening Effects: At high densities or temperatures, gluon interactions are screened, weakening confinement and allowing quarks to behave more like free particles.
- Color Superconductivity: At extremely high densities, quarks may form Cooper pairs (similar to electrons in a superconductor), leading to a color-superconducting phase.
7. Experimental Evidence for QGP
- Heavy-Ion Collisions: Experiments at particle colliders (e.g., RHIC and LHC) create QGP by colliding heavy nuclei at extremely high energies.
- These collisions momentarily recreate the conditions of the early universe, where QGP is believed to have existed.
- Observations show that QGP behaves like a near-perfect fluid, with properties deviating from the simplistic Fermi gas model due to strong interactions.
8. Summary
The Fermi gas model applies to quark-gluon plasmas by describing the behavior of quarks as a degenerate system of fermions:
- Degeneracy pressure from quarks helps counteract gravitational collapse in extreme environments, such as neutron stars with quark cores.
- At high densities, the quarks behave like a relativistic Fermi gas, while at high temperatures, thermal excitations dominate the dynamics.
- Modifications to the ideal Fermi gas model are necessary to account for strong interactions and collective effects in the QGP.
This model is essential for understanding the structure of hybrid stars, the collapse of neutron stars into black holes, and the behavior of matter at the most extreme conditions in the universe. Let me know if you’d like to dive deeper into any specific aspect! 😊
3:15 AM
Assistant
The Fermi gas model does not directly apply to black holes, as black holes are fundamentally different objects governed by the laws of general relativity rather than quantum mechanics or statistical mechanics. However, the concepts behind the Fermi gas model—particularly its role in the physics of degenerate matter—help explain the processes that lead to the formation of black holes.
Here’s how the Fermi gas model connects to black hole formation and the physics of the matter leading up to a black hole’s collapse:
1. The Role of the Fermi Gas Model in Pre-Black Hole States
a. Degenerate Matter in Stellar Remnants
White Dwarfs:
- Electron degeneracy pressure (from a degenerate electron gas) supports white dwarfs against gravitational collapse.
- If the mass of a white dwarf exceeds the Chandrasekhar limit (
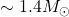 ), electron degeneracy pressure is insufficient to counteract gravity, leading to collapse.
), electron degeneracy pressure is insufficient to counteract gravity, leading to collapse.
Neutron Stars:
- After collapse, a neutron star forms when neutron degeneracy pressure (from a degenerate neutron gas) halts further contraction.
- However, if the mass of the neutron star exceeds the Tolman-Oppenheimer-Volkoff (TOV) limit (
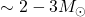 ), even neutron degeneracy pressure cannot resist gravity.
), even neutron degeneracy pressure cannot resist gravity.
b. Collapse Beyond the TOV Limit
- When a stellar remnant exceeds the TOV limit, degeneracy pressure—whether from electrons, neutrons, or quarks—fails to counteract gravity.
- The Fermi gas model, which describes the degeneracy pressure of fermions, is no longer sufficient to prevent collapse.
- The remnant collapses into a black hole, where gravity overwhelms all other forces.
2. Why the Fermi Gas Model Breaks Down in Black Holes
The Fermi gas model assumes:
- Quantum States: Particles occupy discrete quantum states up to a Fermi energy.
- Well-Defined Volume: The system exists within a finite physical volume where particles are not infinitely compressed.
However, in a black hole:
- Event Horizon: The black hole has an event horizon, beyond which no information or matter can escape. This boundary fundamentally changes the physics from that of a Fermi gas.
- Singularity: At the center of a black hole, matter collapses to a point of infinite density (in classical general relativity). The Fermi gas model cannot describe infinite compression, as the underlying assumptions (discrete quantum states and Pauli exclusion) break down.
- Relativity Dominates: General relativity, not quantum mechanics (or the Fermi gas model), governs the behavior of matter and spacetime in and near a black hole.
3. Fermi Gas and the Formation of Black Holes
Although the Fermi gas model does not apply inside a black hole, it is essential in describing the stages leading to black hole formation:
a. Gravitational Collapse of a Massive Star
- In the core of a massive star, nuclear fusion provides thermal pressure to counteract gravity.
- When nuclear fuel is exhausted, the core begins to collapse.
- If the core’s mass exceeds the Chandrasekhar limit:
- Electron degeneracy pressure fails, leading to a neutron star or a black hole.
- If the core’s mass exceeds the TOV limit:
- Neutron degeneracy pressure fails, and the core collapses directly into a black hole.
b. Role of Relativistic Fermi Gas
- As the core collapses, fermions (electrons, neutrons, or quarks) become relativistic, meaning their speeds approach the speed of light.
- The degeneracy pressure of a relativistic Fermi gas (
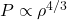 ) grows more slowly with density than that of a non-relativistic Fermi gas (
) grows more slowly with density than that of a non-relativistic Fermi gas (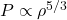 ).
). - This slower growth of pressure is insufficient to balance gravity for masses above the TOV limit, leading to collapse into a black hole.
4. Exotic Matter and Black Hole Formation
a. Quark Matter and Quark Stars
- At extremely high densities, neutrons inside a collapsing core may break down into their constituent quarks, forming a quark-gluon plasma.
- If quark degeneracy pressure (from a Fermi gas of quarks) is sufficient, the core may temporarily form a quark star.
- If the mass exceeds the limit for quark degeneracy pressure, the star collapses into a black hole.
b. Beyond the Fermi Gas Model
The collapse into a black hole may involve exotic physics beyond the Fermi gas model, such as:
- Bose-Einstein condensates of certain particles.
- Quantum gravity effects, which are not yet fully understood.
5. Fermi Gas and Black Hole Physics
While the Fermi gas model does not describe the interior of a black hole, its principles can help in understanding:
Hawking Radiation:
- Near a black hole’s event horizon, quantum effects (including particle-antiparticle pairs) may lead to Hawking radiation. This involves quantum field theory rather than the Fermi gas model but relies on similar quantum principles for particle behavior.
Entropy and Quantum States:
- The Fermi gas model’s description of quantum states contributes to discussions about black hole entropy and the quantum nature of black holes.
6. Summary
The Fermi gas model applies to the pre-collapse stages of black hole formation by describing the behavior of degenerate matter (electrons, neutrons, or quarks) in:
- White dwarfs, where electron degeneracy pressure prevents collapse.
- Neutron stars, where neutron degeneracy pressure supports the star up to the TOV limit.
- Quark stars, where quark degeneracy pressure may temporarily resist collapse.
Once the degeneracy pressure fails (due to exceeding mass limits), the remnant collapses into a black hole, where the Fermi gas model no longer applies. Inside black holes, the physics is dominated by general relativity and potentially quantum gravity, moving beyond the scope of the Fermi gas model.
Let me know if you’d like to explore specific aspects of black hole physics or the transition from Fermi gas-dominated systems to black holes! 😊
3:27 AM


Recent Comments