Strong Spin–Orbit Coupling in Nuclear Physics
In nuclear physics, strong spin–orbit coupling is the crucial interaction that makes the nuclear shell model work and explains the observed magic numbers. Below is a clear, step-by-step explanation of what it is, why it is “strong,” and what it does.
1. What “Spin–Orbit” Means
Every nucleon (proton or neutron) has:
- Orbital angular momentum
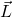 — due to its motion inside the nucleus
— due to its motion inside the nucleus - Intrinsic spin
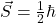
The spin–orbit interaction couples these two:
![]()
This term shifts the energy depending on whether the spin is:
- Aligned with
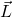 →
→ 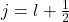
- Anti-aligned with
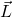 →
→ 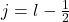
2. Why Spin–Orbit Is “Strong” in Nuclei
In atoms:
- Spin–orbit coupling comes from relativistic corrections to the Coulomb interaction
- It is relatively weak
In nuclei:
- The interaction arises from the strong nuclear force, not electromagnetism
- The potential is deep (~50 MeV)
- Nucleons move at fast (relativistic) speeds
- The nuclear force has a strong tensor component
Result: Spin–orbit splitting in nuclei is an order of magnitude larger than in atoms.
| Atomic Spin–Orbit | Nuclear Spin–Orbit | |
|---|---|---|
| Strength | eV scale | MeV scale |
| Origin | Electromagnetic (relativistic) | Strong nuclear force |
3. Mathematical Form (Qualitative)
A typical nuclear shell-model Hamiltonian includes:
![]()
Where:
![]()
Key point: The nuclear potential has a sharp surface → ![]() is large near the surface →
is large near the surface → ![]() is very strong.
is very strong.
4. Energy Level Splitting
For each orbital ![]() , spin–orbit coupling splits levels into two:
, spin–orbit coupling splits levels into two:
| Orbital | Levels |
|---|---|
Crucially: The ![]() level is much lower in energy.
level is much lower in energy.
This downward shift of the higher-![]() state creates large energy gaps and rearranges shell closures.
state creates large energy gaps and rearranges shell closures.
5. Creation of Magic Numbers
Without spin–orbit:
![]()
With strong spin–orbit:
![]()
Example: The large downward shift of the ![]() level creates the shell closure at 28. Similar effects produce 50, 82, and 126.
level creates the shell closure at 28. Similar effects produce 50, 82, and 126.
No strong spin–orbit → no correct magic numbers!
6. Physical Intuition
A useful picture:
- A nucleon moves through a strong, rapidly changing nuclear potential
- In its rest frame, motion through the nuclear field produces an effective magnetic field
- This field couples strongly to the nucleon’s spin
- Alignment lowers energy; anti-alignment raises it
Though this analogy borrows from electromagnetism, the force is the strong interaction, so the effect is much larger.
7. Experimental Evidence
Strong spin–orbit coupling is confirmed by:
- Large splittings between
 levels
levels - Correct prediction of magic numbers
- Nuclear spectroscopy
- Scattering experiments
- Binding energy systematics
8. Why This Was a Big Deal
Before 1949: The shell model failed beyond 20.
After Mayer & Jensen added strong spin–orbit coupling:
- Magic numbers explained
- Nuclear structure made sense
- Nobel Prize in Physics (1963)
This is considered one of the great breakthroughs of 20th-century nuclear physics.
9. Key Differences from Atomic Spin–Orbit
- Electromagnetic origin
- Weak (eV)
- Relativistic correction
- Small shell effects
- Strong-force origin
- Strong (MeV)
- Dominant interaction
- Determines shell structure
Strong spin–orbit coupling in nuclei arises from the strong nuclear force acting in a steep, short-range potential, producing large energy splittings between


Recent Comments