Magnetic Field Increase at Relativistic Speeds

by | Oct 18, 2025 | Uncategorized | 0 comments

Thomas Lee Abshier
Author: Thomas Lee Abshier

Is there an increase in the magnetic field in charged particles at relativistic speeds, related to gamma?

Yes, the magnetic field produced by a charged particle does increase in specific directions as the particle approaches relativistic speeds, and this is linked to the Lorentz factor (\gamma).

The effect arises due to the relativistic transformation of electromagnetic fields and the fact that the motion of a charged particle at high speeds results in a stronger magnetic field in directions perpendicular to its motion. Here’s a detailed explanation:

1. Electromagnetic Field of a Moving Charged Particle

For a charged particle moving at a velocity v, the electric (E) and magnetic (B) fields it generates depend on its motion relative to an observer. At relativistic speeds (v close to c, the speed of light), relativistic effects, governed by the Lorentz factor \gamma = \frac{1}{\sqrt{1 - v^2 / c^2}}, significantly alter the field structure.

  • v: Velocity of the charged particle.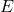
  • E: Electric field.
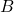  • B: Magnetic field.
  • c: Speed of light.
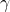  • \gamma: Lorentz factor.

Key Relativistic Effects:

  • The electric field (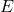E) becomes compressed in the direction perpendicular to the particle’s motion, leading to a stronger field in those directions.
  • The motion of the charge generates a magnetic field (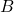B) whose strength depends on the velocity of the charge.

2. Magnetic Field and the Lorentz Factor

The magnetic field generated by a moving charge is proportional to its velocity, which increases with v. For a relativistic charged particle, the magnetic field strength in a direction perpendicular to the motion is enhanced by the Lorentz factor \gamma. Specifically:

Magnetic Field in the Perpendicular Plane:

In the plane perpendicular to the particle’s motion, the magnetic field is stronger at relativistic speeds because the electric field is compressed in this direction and the velocity is higher.

The magnitude of the magnetic field in this plane scales roughly as:

B \propto \frac{\gamma v}{r^2}

where r is the distance from the particle.

  • r: Distance from the particle.

Magnetic Field in the Parallel Direction:

In the direction parallel to the motion, the magnetic field is weaker and does not grow as significantly because the compression of the electric field occurs mainly in the perpendicular plane.

3. Relativistic Electrodynamics

The relationship between the electric field and magnetic field of a moving charge can be understood from relativistic electrodynamics. In the rest frame of the charge:

  • The particle produces only an electric field (E).

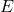When viewed from a frame where the charge is in motion, this electric field transforms into both an electric field and a magnetic field (B).

The relativistic transformation of fields is governed by the equations:

B = \frac{v \times E}{c^2}

where v is the velocity of the particle. At relativistic speeds (v \approx c), the magnetic field grows stronger in proportion to the velocity.

4. Directional Dependence and 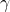\gamma Scaling

The field structure of a relativistic charged particle can be summarized as follows:

  • In the rest frame of the particle, the electric field is isotropic (spherically symmetric).
  • In the lab frame (where the charge is moving at relativistic speeds), the fields are distorted:
  • The electric field is compressed in the direction perpendicular to the motion, scaling as \gamma.
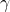  • The generated magnetic field also scales with 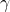\gamma, particularly in the perpendicular direction.

Thus, for a charged particle moving at relativistic velocities, the magnetic field strength increases significantly in the perpendicular direction, and the increase is directly related to \gamma = \frac{1}{\sqrt{1 - v^2 / c^2}}.

5. Application and Observational Effects

This relativistic enhancement of the magnetic field has important consequences in high-energy physics and astrophysics:

  • Synchrotron Radiation: Electrons moving at relativistic speeds in magnetic fields (e.g., in particle accelerators or astrophysical jets) emit synchrotron radiation. The relativistic increase in the magnetic field strength contributes to the high energy of the emitted photons.
  • Relativistic Beaming: The compression of the electric and magnetic fields in the perpendicular plane leads to the highly directional nature of radiation from relativistic particles.

Summary

At relativistic speeds, the magnetic field produced by a charged particle increases in the directions perpendicular to its motion, and this increase is proportional to the Lorentz factor (\gamma). This effect arises due to relativistic transformations of the electric and magnetic fields, which compress the fields in the perpendicular direction and enhance the magnetic component.

Submit a Comment