The Lagrangian

by | Oct 17, 2025 | Physics | 0 comments

Thomas Lee Abshier
Author: Thomas Lee Abshier

What is a Lagrangian?

In physics, a Lagrangian is a mathematical function that describes the dynamics of a physical system. It is central to Lagrangian mechanics, one of the formulations of classical mechanics, and it also plays a key role in quantum mechanics, quantum field theory, and general relativity.

At its core, the Lagrangian encodes the laws of motion of a system by balancing the kinetic energy and potential energy, and it is used to derive the equations of motion for the system through the principle of least action (or stationary action).

Mathematical Definition

For a system with generalized coordinates q_i(t) and their time derivatives \dot{q}_i(t), the Lagrangian L is defined as:

L(q_i, \dot{q}_i, t) = T - V

Where:

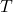  • T: Kinetic energy of the system.
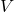  • V: Potential energy of the system.

Key Concepts of the Lagrangian

Action:

The action S is the integral of the Lagrangian over time:

S = \int L \, dt

The principle of least action states that the path taken by a physical system between two points in time is the one that minimizes (or makes stationary) the action S.

Euler-Lagrange Equations:

From the Lagrangian, the equations of motion are derived using the Euler-Lagrange equations:

\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = 0

These equations describe the time evolution of the system’s generalized coordinates q_i(t).

Generalization to Fields:

In field theory, the Lagrangian describes systems in terms of fields \phi(x, t) rather than discrete particles. The Lagrangian density L is used, and the action becomes:

S = \int L \, d^4 x

Here, d^4 x is the spacetime volume element.

Example: Classical Mechanics

For a simple particle of mass m in a potential V(x), the Lagrangian is:

L = T - V = \frac{1}{2} m \dot{x}^2 - V(x)

The Euler-Lagrange equation for this Lagrangian recovers Newton’s second law:

m \ddot{x} = -\frac{d V}{d x}

Lagrangians in Advanced Physics

Lagrangians are also fundamental in describing more complex systems:

Wave Equations:

The dynamics of waves, such as electromagnetic waves, can be derived from a Lagrangian density. For example, the Lagrangian for the electromagnetic field E, B is:

L = \frac{1}{2} (E^2 - B^2)

Quantum Field Theory (QFT):

In Quantum Field Theory (QFT), the Lagrangian density L governs the dynamics of quantum fields, such as the Klein-Gordon field or the Dirac field.

General Relativity:

The dynamics of spacetime are described by the Einstein-Hilbert Lagrangian:

L = R

where R is the Ricci scalar curvature.

Submit a Comment