What is the Planck Energy?
The Planck energy is the unit of energy in the system of natural units known as Planck units, which are derived from fundamental constants of nature. It represents an extremely large amount of energy and is important in theoretical physics, particularly in the study of quantum gravity and the unification of quantum mechanics with general relativity.
Definition of Planck Energy
The Planck energy is defined as:
![]()
where:
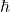 : reduced Planck’s constant (
: reduced Planck’s constant (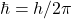 ),
), : speed of light in a vacuum,
: speed of light in a vacuum,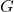 : gravitational constant.
: gravitational constant.
Value of the Planck Energy
The numerical value of the Planck energy in standard units is:
![]() Joules (J)
Joules (J)
or
![]() GeV (giga-electronvolts).
GeV (giga-electronvolts).
This is an immense amount of energy by everyday standards. For comparison:
- The kinetic energy of a car traveling at highway speeds is on the order of
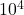 J.
J. - A lightning bolt has an energy of about
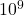 J, similar to the Planck energy.
J, similar to the Planck energy.
Significance of the Planck Energy
The Planck energy plays a crucial role in theoretical physics, particularly in areas where quantum mechanics and general relativity intersect. Its significance includes:
- Threshold for Quantum Gravity:
- The Planck energy corresponds to the energy scale at which quantum gravitational effects are expected to become significant.
- At this energy, the effects of spacetime curvature (described by general relativity) and quantum uncertainty (from quantum mechanics) are equally important.
- A theory of quantum gravity, such as string theory or loop quantum gravity, is needed to describe physics at this energy scale.
- Planck Scale:
- The Planck energy is part of the “Planck scale,” which includes the Planck length (
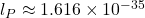 m) and Planck time (
m) and Planck time (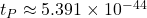 s).
s). - These scales set the boundaries for our current understanding of the universe. For example, phenomena smaller than the Planck length or shorter than the Planck time cannot be described by classical physics or quantum field theory.
- The Planck energy is part of the “Planck scale,” which includes the Planck length (
- Big Bang and Cosmology:
- The Planck energy is thought to correspond to the energy density of the universe in the moments immediately after the Big Bang (the so-called Planck epoch).
- Understanding physics at this scale is essential for explaining the earliest moments of the universe and the origin of fundamental forces.
How the Planck Energy is Derived
The Planck energy is obtained from dimensional analysis using fundamental constants:
- The gravitational constant,
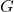 , introduces the effects of gravity.
, introduces the effects of gravity. - The speed of light,
 , relates to relativistic effects.
, relates to relativistic effects. - The reduced Planck’s constant,
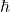 , relates to quantum effects.
, relates to quantum effects.
By combining these constants, we obtain a natural unit of energy that is independent of human-defined measurement systems (like kilograms or meters).
Practical Considerations
While the Planck energy is critical in theoretical physics, it is far beyond the reach of current experimental capabilities:
- The highest-energy particle collisions achieved at the Large Hadron Collider (LHC) reach about
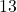 TeV (
TeV (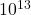 eV), which is six orders of magnitude below the Planck energy (
eV), which is six orders of magnitude below the Planck energy (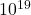 GeV).
GeV).
Thus, while the Planck energy is a theoretical concept, it serves as a guide for future advances in high-energy physics.
Summary
The Planck energy (![]() ) is a fundamental unit of energy defined as
) is a fundamental unit of energy defined as ![]() , with a value of approximately
, with a value of approximately ![]() J or
J or ![]() GeV. It marks the energy scale where quantum gravity effects dominate, and it is critical for understanding the earliest universe, black holes, and the unification of quantum mechanics with general relativity.
GeV. It marks the energy scale where quantum gravity effects dominate, and it is critical for understanding the earliest universe, black holes, and the unification of quantum mechanics with general relativity.
What is the Compton wavelength of an electron?
The Compton wavelength of a particle, such as an electron, is a fundamental physical constant that describes a characteristic quantum length scale associated with the particle. It is the wavelength of a photon whose energy is equivalent to the rest energy of the particle.
Definition
The Compton wavelength (![]() ) is given by:
) is given by:
![]()
where:
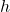 : Planck’s constant (
: Planck’s constant (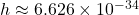 J
J s),
s),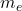 : mass of the electron (
: mass of the electron (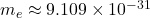 kg),
kg), : speed of light in a vacuum (
: speed of light in a vacuum (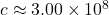 m/s).
m/s).
Value of the Electron’s Compton Wavelength
Substituting the constants into the formula:
![]()
![]() m
m
So, the Compton wavelength of an electron is approximately:
![]() picometers (pm)
picometers (pm)
or
![]() m.
m.
Physical Meaning
- Quantum Limit of Localization:
- The Compton wavelength represents a limit on how precisely you can localize a particle in space without creating a particle-antiparticle pair (via quantum mechanics and special relativity).
- If you try to confine an electron to a region smaller than its Compton wavelength, the uncertainty in its momentum becomes so large that the energy exceeds the electron’s rest energy (
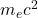 ) and can create an electron-positron pair.
) and can create an electron-positron pair.
- Interaction with Photons:
- The Compton wavelength appears in Compton scattering, where a photon scatters off an electron. The scattering results in a shift in the wavelength of the photon, which depends on the Compton wavelength.
- Scale of Quantum Effects:
- The Compton wavelength gives a sense of the quantum scale at which relativistic effects become important for a particle. For an electron, this scale is on the order of
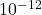 m.
m.
- The Compton wavelength gives a sense of the quantum scale at which relativistic effects become important for a particle. For an electron, this scale is on the order of
Comparison with Other Length Scales
The Compton wavelength of the electron (![]() pm) is much smaller than the Bohr radius (
pm) is much smaller than the Bohr radius (![]() Å, or
Å, or ![]() m), which is the typical size of an atom.
m), which is the typical size of an atom.
It is also larger than the Planck length (![]() m), which is the scale where quantum gravity effects become significant.
m), which is the scale where quantum gravity effects become significant.
Summary
The Compton wavelength of an electron is ![]() pm. It represents a fundamental quantum length scale, related to the rest energy of the electron, and plays a key role in quantum mechanics and high-energy physics, especially in phenomena involving photons and electrons.
pm. It represents a fundamental quantum length scale, related to the rest energy of the electron, and plays a key role in quantum mechanics and high-energy physics, especially in phenomena involving photons and electrons.
How is the Compton wavelength derived?
The Compton wavelength is derived by equating the energy of a photon (given by its wavelength) to the rest energy of a particle (such as an electron). Here’s a step-by-step explanation of the derivation:
-
- Rest Energy of a Particle
The rest energy of a particle is given by Einstein’s famous equation:
![]()
where:
-
-
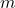 : the rest mass of the particle,
: the rest mass of the particle, : the speed of light,
: the speed of light,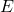 : the rest energy.
: the rest energy.
- Energy of a Photon
-
The energy of a photon is related to its wavelength by the equation:
![]()
where:
-
-
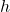 : Planck’s constant (
: Planck’s constant (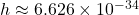 J
J s),
s),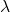 : the wavelength of the photon,
: the wavelength of the photon, : the speed of light.
: the speed of light.
- Equating the Two Energies
-
To find the Compton wavelength, we consider a photon whose energy is equivalent to the rest energy of the particle. Thus, we set the two expressions for energy equal to each other:
![]()
-
- Solve for Wavelength
Rearranging this equation for ![]() , we find:
, we find:
![]()
This wavelength, ![]() , is known as the Compton wavelength of the particle.
, is known as the Compton wavelength of the particle.
-
- The Compton Wavelength of an Electron
For the electron, substituting the known constants:
-
-
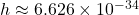 J
J s,
s,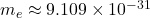 kg,
kg,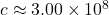 m/s,
m/s,
-
we get:
![]() m.
m.
So the Compton wavelength of an electron is approximately:
![]() picometers (pm).
picometers (pm).
Physical Interpretation
The Compton wavelength represents the smallest possible wavelength of a photon that can interact with a particle at rest and transfer enough energy to excite or create a similar particle (e.g., via particle-antiparticle pair production). It is a fundamental quantum limit for localizing a particle in space.
Applications
- Compton Scattering: In scattering processes, the change in the wavelength of a photon depends on the Compton wavelength.
- Quantum Mechanics: The Compton wavelength sets a limit on how precisely a particle’s position can be localized without creating new particles.
- High-Energy Physics: It provides a natural length scale for quantum and relativistic effects.
How are the de Broglie wavelength and Compton wavelength different?
The de Broglie wavelength and the Compton wavelength are both fundamental concepts in quantum mechanics, but they describe very different physical phenomena. Here’s a detailed comparison to highlight their differences:
-
- Definitions
de Broglie Wavelength
The de Broglie wavelength is associated with the wave-like behavior of a particle in motion and is given by:
![]()
where:
-
-
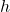 : Planck’s constant,
: Planck’s constant,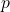 : the particle’s momentum (
: the particle’s momentum (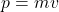 , for non-relativistic motion).
, for non-relativistic motion).
-
The de Broglie wavelength is inversely proportional to the momentum of the particle and depends on the particle’s velocity.
Compton Wavelength
The Compton wavelength is a fundamental quantum property of a particle and is related to its rest mass. It is given by:
![]()
where:
-
-
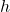 : Planck’s constant,
: Planck’s constant,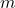 : the rest mass of the particle,
: the rest mass of the particle, : the speed of light.
: the speed of light.
-
The Compton wavelength depends only on the particle’s rest mass and is a fixed property for a given particle.
-
- Physical Meaning
de Broglie Wavelength
The de Broglie wavelength represents the wavelength of the matter wave associated with a particle (wave-particle duality).
It applies to particles in motion, such as electrons, protons, or even macroscopic objects, and depends on the particle’s velocity and momentum.
For slow-moving particles (low momentum), the de Broglie wavelength is large, while for fast-moving particles, it becomes smaller.
Compton Wavelength
The Compton wavelength is a measure of the quantum “size” of a particle and represents a fundamental limit on how precisely the particle can be localized in space without creating a particle-antiparticle pair.
It arises in interactions between photons and particles, such as Compton scattering.
Unlike the de Broglie wavelength, the Compton wavelength does not depend on the particle’s velocity or momentum; it is a fixed property for a particle determined by its mass.
-
- Key Differences
Table: Comparison of de Broglie and Compton Wavelengths
| Property | de Broglie Wavelength | Compton Wavelength |
|---|---|---|
| Formula | ||
| Depends on Momentum? | Yes, inversely proportional to the particle’s momentum. | No, depends only on the particle’s rest mass. |
| Depends on Velocity? | Yes, |
No, independent of velocity or momentum. |
| Physical Meaning | Wavelength of the particle’s matter wave. | Fundamental quantum scale of the particle. |
| Applies to | Any particle in motion. | A particle at rest (fixed property of mass). |
| Order of Magnitude | Can vary widely depending on momentum. | Fixed for a given particle, e.g., |
| Context | Wave-particle duality and quantum mechanics. | Quantum electrodynamics and relativistic effects. |
-
- Practical Examples
de Broglie Wavelength
For an electron moving at a velocity of ![]() m/s:
m/s:
![]() kg
kg![]() m/s.
m/s.
![]() m.
m.
This is on the order of the size of an atom, so the de Broglie wavelength is relevant for describing quantum phenomena in atoms.
Compton Wavelength
For an electron, the Compton wavelength is:
![]() m.
m.
This is much smaller than the de Broglie wavelength of a slow-moving electron and represents the scale at which relativistic quantum effects become significant (e.g., Compton scattering).
-
- When Do They Matter?
de Broglie Wavelength:
-
-
- Applicable when studying the wave-like behavior of particles, such as in electron diffraction or quantum mechanics.
- Important for low-momentum particles, where the wavelength can be large.
-
Compton Wavelength:
-
- Relevant in high-energy physics and quantum electrodynamics, particularly in interactions involving photons and particles (e.g., Compton scattering).
- Sets a quantum limit to the precision with which a particle’s position can be measured.
Summary
The de Broglie wavelength is associated with a particle’s momentum and describes its wave-particle duality.
The Compton wavelength is a fundamental property of a particle, depending only on its rest mass, and describes the quantum limit of localization.
The two wavelengths are conceptually and mathematically distinct, but both are crucial in understanding quantum mechanics and high-energy physics.


Recent Comments