The Speed of Light’s Relationship to 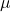 and
and 
By Thomas Lee Abshier, ND, and Poe Assistant
7/29/2025
The relationship between the speed of light (![]() ) and the permeability (
) and the permeability (![]() ) and permittivity (
) and permittivity (![]() ) of free space arises from the fundamental nature of electromagnetic waves, as described by Maxwell’s equations. The formula is:
) of free space arises from the fundamental nature of electromagnetic waves, as described by Maxwell’s equations. The formula is:
![]()
This equation shows that the speed of light depends on the electromagnetic properties of the vacuum: the ability of the vacuum to support electric fields (![]() ) and magnetic fields (
) and magnetic fields (![]() ).
).
 : speed of light
: speed of light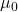 : vacuum permeability
: vacuum permeability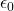 : vacuum permittivity
: vacuum permittivity
1. What are 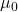 and
and 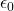 ?
?
Vacuum Permittivity (![]() ):
):
A measure of how easily an electric field can form in a vacuum.
It determines the strength of the electric field generated by a given electric charge in free space.
Units: F/m (farads per meter).
Vacuum Permeability (![]() ):
):
A measure of how easily a magnetic field can form in a vacuum.
It determines the strength of the magnetic field generated by electric currents or changing electric fields in free space.
Units: H/m (henries per meter).
2. How Do 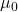 and
and 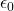 Relate to the Speed of Light?
Relate to the Speed of Light?
The connection arises from Maxwell’s equations, which describe the behavior of electric and magnetic fields. Specifically:
Electromagnetic Waves:
Maxwell’s equations predict that a changing electric field generates a magnetic field, and vice versa. This mutual generation creates a self-sustaining electromagnetic wave that propagates through space.
The equations lead to a wave equation for electric and magnetic fields, with a propagation speed (![]() ) given by:
) given by:
![]()
 : speed of light
: speed of light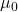 : vacuum permeability
: vacuum permeability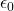 : vacuum permittivity
: vacuum permittivity
Physical Meaning:
![]() determines how the electric field varies in response to charges in free space.
determines how the electric field varies in response to charges in free space.
![]() determines how the magnetic field varies in response to currents or changing electric fields.
determines how the magnetic field varies in response to currents or changing electric fields.
Together, they set the “stiffness” of spacetime to support electromagnetic waves, dictating the speed at which these waves travel.
3. Why Does This Relationship Exist?
The relationship between ![]() ,
, ![]() , and
, and ![]() comes directly from the structure of Maxwell’s equations. Here’s why:
comes directly from the structure of Maxwell’s equations. Here’s why:
a. Wave Equation Derivation
From Maxwell’s equations in free space:
Faraday’s law: A time-varying magnetic field produces a circulating electric field:
![]()
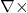 : curl operator
: curl operator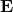 : electric field
: electric field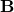 : magnetic field
: magnetic field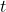 : time
: time
Ampere’s law (in free space): A time-varying electric field produces a circulating magnetic field:
![]()
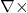 : curl operator
: curl operator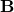 : magnetic field
: magnetic field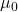 : vacuum permeability
: vacuum permeability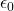 : vacuum permittivity
: vacuum permittivity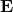 : electric field
: electric field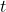 : time
: time
Taking the curl of Faraday’s law and substituting Ampere’s law into it leads to a wave equation for the electric field:
![]()
 : Laplacian operator
: Laplacian operator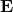 : electric field
: electric field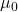 : vacuum permeability
: vacuum permeability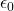 : vacuum permittivity
: vacuum permittivity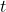 : time
: time
This is a wave equation, and the term ![]() represents the speed of the wave, which is
represents the speed of the wave, which is ![]() , the speed of light.
, the speed of light.
b. Impedance of Free Space
The product of ![]() and
and ![]() also determines the “impedance” of free space, which describes how electric and magnetic fields relate in an electromagnetic wave:
also determines the “impedance” of free space, which describes how electric and magnetic fields relate in an electromagnetic wave:
![]()
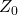 : impedance of free space
: impedance of free space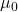 : vacuum permeability
: vacuum permeability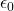 : vacuum permittivity
: vacuum permittivity
This impedance governs the interaction of electromagnetic waves with matter.
4. Intuition: What Do 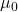 and
and 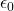 “Do”?
“Do”?
Imagine the vacuum as a medium that supports electromagnetic waves:
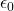 : Determines how “permissive” the vacuum is to the formation of electric fields. A larger
: Determines how “permissive” the vacuum is to the formation of electric fields. A larger 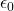 means the electric field builds up more slowly in response to a charge.
means the electric field builds up more slowly in response to a charge.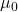 : Determines how “reactive” the vacuum is to the formation of magnetic fields. A larger
: Determines how “reactive” the vacuum is to the formation of magnetic fields. A larger 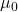 means magnetic fields take more effort to form.
means magnetic fields take more effort to form.
The interplay between these two constants determines how quickly electromagnetic waves propagate:
If ![]() or
or ![]() were larger, the wave would propagate more slowly.
were larger, the wave would propagate more slowly.
If they were smaller, the wave would propagate more quickly.
5. Universal Constants and 
The speed of light is a fundamental constant of nature (![]() m/s). Its value depends on
m/s). Its value depends on ![]() and
and ![]() , but these constants themselves are tied to the structure of spacetime and the laws of physics.
, but these constants themselves are tied to the structure of spacetime and the laws of physics.
 : speed of light
: speed of light : approximately
: approximately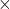 : multiplication
: multiplication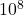 : ten to the power of eight
: ten to the power of eight
Vacuum Permeability (![]() ):
):
By definition, ![]() H/m in the SI system. This is a convention chosen to simplify electromagnetic equations.
H/m in the SI system. This is a convention chosen to simplify electromagnetic equations.
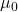 : vacuum permeability
: vacuum permeability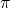 : pi
: pi : multiplication
: multiplication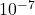 : ten to the power of negative seven
: ten to the power of negative seven
Vacuum Permittivity (![]() ):
):
Derived from the relationship:
![]()
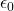 : vacuum permittivity
: vacuum permittivity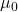 : vacuum permeability
: vacuum permeability : speed of light
: speed of light
This interdependence means that ![]() ,
, ![]() , and
, and ![]() are not independent, but reflect the fundamental properties of spacetime.
are not independent, but reflect the fundamental properties of spacetime.
6. Summary
The speed of light (![]() ) is related to
) is related to ![]() (vacuum permeability) and
(vacuum permeability) and ![]() (vacuum permittivity) because these constants describe the ability of free space to support electric and magnetic fields. Together, they set the “stiffness” of spacetime for electromagnetic waves, determining how fast these waves propagate.
(vacuum permittivity) because these constants describe the ability of free space to support electric and magnetic fields. Together, they set the “stiffness” of spacetime for electromagnetic waves, determining how fast these waves propagate.
Mathematically:
![]()
and this relationship is a direct consequence of Maxwell’s equations, which govern the behavior of electric and magnetic fields.
 : speed of light
: speed of light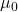 : vacuum permeability
: vacuum permeability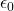 : vacuum permittivity
: vacuum permittivity


Recent Comments